Число круче, чем π

Вопрос о том, кто открыл число е, до сих пор вызывает споры. Долгое время математики, фактически пользуясь этим числом, никак не могли его распознать. Однако потрясающая особенность е появляться в самых неожиданных контекстах и помогать с описанием самых разных природных, технических, экономических и демографических процессов привела к тому, что на сегодняшний день нет, пожалуй, области знаний, где бы оно не использовалось, а некоторые науки обязаны ему значительными успехами.
Прячущееся в логарифмах
Число е пришло в математику достаточно поздно, поскольку не имело геометрического происхождения в отличие от π, √2 или золотого сечения, известных ещё с древности. Неявно оно появилось практически одновременно с изобретением логарифмов в 1614 году, как основание одного из видов логарифмов, который лишь через полвека получил название натурального. Правда, у «отца» логарифмов шотландского математика Джона Непера логарифм был не совсем натуральный (его основание близко к 1/е), но уже в 1618 году в приложении к переводу его труда на английский язык появилась табличка из нескольких натуральных логарифмов, сделанная, вероятно, английским математиком и изобретателем логарифмической линейки Уильямом Отредом. А на следующий год другой англичанин, математик и преподаватель Джон Спейделл издал таблицы натуральных логарифмов чисел от 1 до 1000 и синусов под названием «Новые логарифмы…». В 1624 году создатель первых таблиц десятич-ных логарифмов профессор математики в Оксфорде Генри Бригс вычислил коэффициент, позволяющий связать десятичные логарифмы с натуральными. Фактически это был десятичный логарифм е.
Однако само число е тогда введено не было. Дело в том, что алгоритмы вычисления логарифмов того времени (см. статью «Его величество логарифм», «Наука и жизнь» № 5, 2020 г.) не предусматривали понятия их основания. То, что вычисляемые в те годы логарифмы были по основаниям десять (десятичные) или е (натуральные), стало понятно значительно позже. Более того, даже связь логарифмов с показателями степеней (y = logex; x = ey), с которой начинается их изучение в современной школе, была обнаружена значительно позже. Точно известно, что эту связь в 1684 году уже знал шотландский математик Джеймс Грегори, которого Исаак Ньютон называл в числе своих учителей и вдохновителей. Так что, когда в наше время е называют неперовым числом — это не вполне корректно. Непер не знал этого числа и даже не изобрёл собственно натуральный логарифм.
Любопытно, что термин «экспонента», сейчас прочно связанный с е, появился ещё раньше. Первым, кто использовал слово exponent в значении «показатель степени», был немецкий математик Михаэль Штифель — это понятие встречается в его книге «Arithmetica integra», вышедшей в 1544 году. Именно Штифель, по сути, предложил алгоритм вычисления логарифмов на основе сопоставления арифметической и геометрической прогрессий, использованный Непером. Но поскольку сам Штифель никаких вычислений не сделал, то слава первооткрывателя досталась шотландцу.
Слово «экспонента» происходит от латинского exponentis — «показывающий». Термин экспоненциальная, или показательная функция (кривая) для зависимости y = ax ввёл Лейбниц в 1679 году. В настоящее время функцию y = ax принято называть показательной, а название экспоненциальная функция (экспонента) закреплено за y = ex.
Логарифмы в отсутствии вычислительных машин играли огромную роль в вычислениях, облегчая и упрощая их. Неудивительно, что они были объектом пристального внимания многих учёных, в том числе фигур первой величины — Иоганна Кеплера, Исаака Ньютона, Готфрида Лейбница и Христиана Гюйгенса.
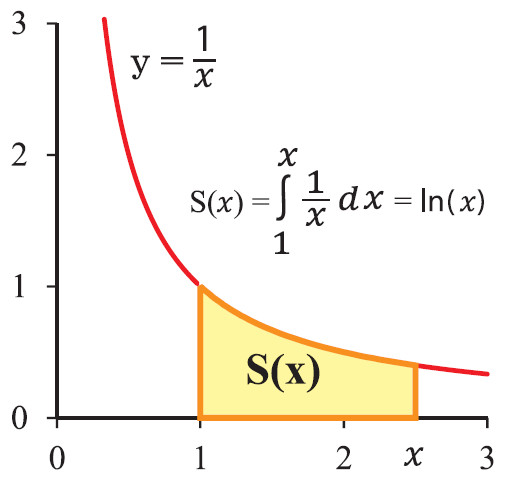
В 1649 году бельгийский математик Грегуар де Сен-Венсан выяснил, что площадь фигуры, ограниченной осью х и гиперболой y = 1/x, изменяется от х по логарифмическому закону. С его лёгкой руки такие логарифмы стали называть гиперболическими. Однако никто тогда не догадался посмотреть, при каком x площадь такой фигуры равна 1 (а это будет как раз при x = e), так что e и в этот раз найдено не было.
В 1668 году благодаря фундаментальному труду «Logarithmotechnia» немецкого математика Николаса Меркатора в научный язык входит термин «натуральный логарифм», но неуловимое число е по-прежнему остаётся в тени. (Кстати, современное обозначение «ln» по первым буквам слов «логарифм» и «натуральный» появилось лишь через 200 лет, в 1893 году его ввёл американский математик Ирвинг Стрингхем.)
Число е как предел
Первым число е неожиданно вычислил швейцарский математик Якоб Бернулли, решая задачу, никак не связанную с логарифмами. В 1690 году он опубликовал исследование так называемого сложного процента — дохода, составляющего определённый процент (р — процентная ставка, доля) от предоставляемой суммы денежных средств. При каждом очередном его вычислении учитывается исходная сумма вместе с начисленными ранее процентами. Таким образом, исходная сумма S0 после n начислений превращается в
S = (1 + p)n · S0.
Например, при годовой процентной ставке 100% (р = 1) исходная сумма по истечении года (n = 1) удваивается, и каждый рубль превращается в два. Но что будет с полученным доходом, если начислять процент чаще, но во столько же раз уменьшать процентную ставку? Например, если каждые полгода начислять по 50% (р = 0,5), то в конце года у вас вместо 1 рубля будет:
S = (1 + ½)2 · 1 руб. = 2,25 руб.
А если начислять каждый месяц, то
S = (1 + 1/12)12 · 1 руб. = 2,261303… руб.
Бернулли показал, что если частоту начисления процентов увеличивать бесконечно, то величина (1 + 1/n)n имеет предел, лежащий между 2,5 и 3. Это была первая грубая оценка числа е. Бернулли не представлял всей значимости полученного им результата, а потому не стал проводить длительные трудоёмкие вычисления, определяя это значение более точно. Он даже не дал ему никакого обозначения. А ведь именно этот предел теперь служит в математике определением числа е. В со-временных обозначениях:
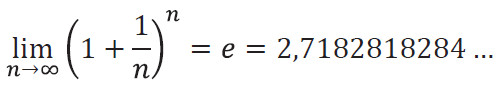
Именно такую сумму даст 1 рубль за год, если начислять процент непрерывно.
Имя Якоба Бернулли также связано с натуральным логарифмом и числом e через изученные им свойства различных кривых. Правда, их связи с найденным пределом он не увидел, возможно, просто не успел, поскольку скончался в возрасте 50 лет. Любимым объектом изучения Бернулли стала так называемая логарифмическая спираль, современная формула которой записывается как ln r = kθ или r = aebθ, где a, b и k — константы. Именно Бернулли первым начал широко использовать при построении кривых полярные координаты (в них положение точки на плоскости описывается двумя числами: радиусом r и углом θ).
В отличие от спирали Архимеда, где витки идут через одинаковое расстояние, витки логарифмической спирали расходятся (расстояние между ними увеличивается). Она часто встречается в природе, её можно обнаружить в строении живых организмов, ураганов и даже галактик. Нашла логарифмическая спираль своё место и в искусстве как способ построения орнаментов и композиций. Так, великий художник эпохи Возрождения Альбрехт Дюрер посвятил ей труд, где показывал, как строить и применять спираль для вычерчивания волют (завитков) капителей, побегов с листвой или украшений епископского жезла.



Сейчас даже трудно представить, с какими сложностями сталкивались исследователи того времени, не имея в своём распоряжении современных форм математической записи и средств математического анализа. Задачи, которые в наше время за считаные минуты решит студент-первокурсник, требовали от них месяцев напряжённой работы и совершения открытий.
Логарифмическая спираль настолько восхитила Бернулли своими свойствами, что он называл её «spira mirabilis» — «удивительная спираль» и даже завещал выбить её на своём надгробии вместе с надписью «EADEM MUTATA RESURGO» («изменённая, я возрождаюсь такой же»), которая описывает свойство этой кривой сохранять свою форму после некоторых преобразований. Правда, тут история немного пошутила над математиком, необразованный мастер изобразил на надгробии спираль Архимеда…
