Рождение легенды
— Нет, Холмс, вы не человек, вы арифмометр! — воскликнул я. Артур Конан Дойл. Знак четырёх (1890)

Фото: www.tekniskamuseet.se
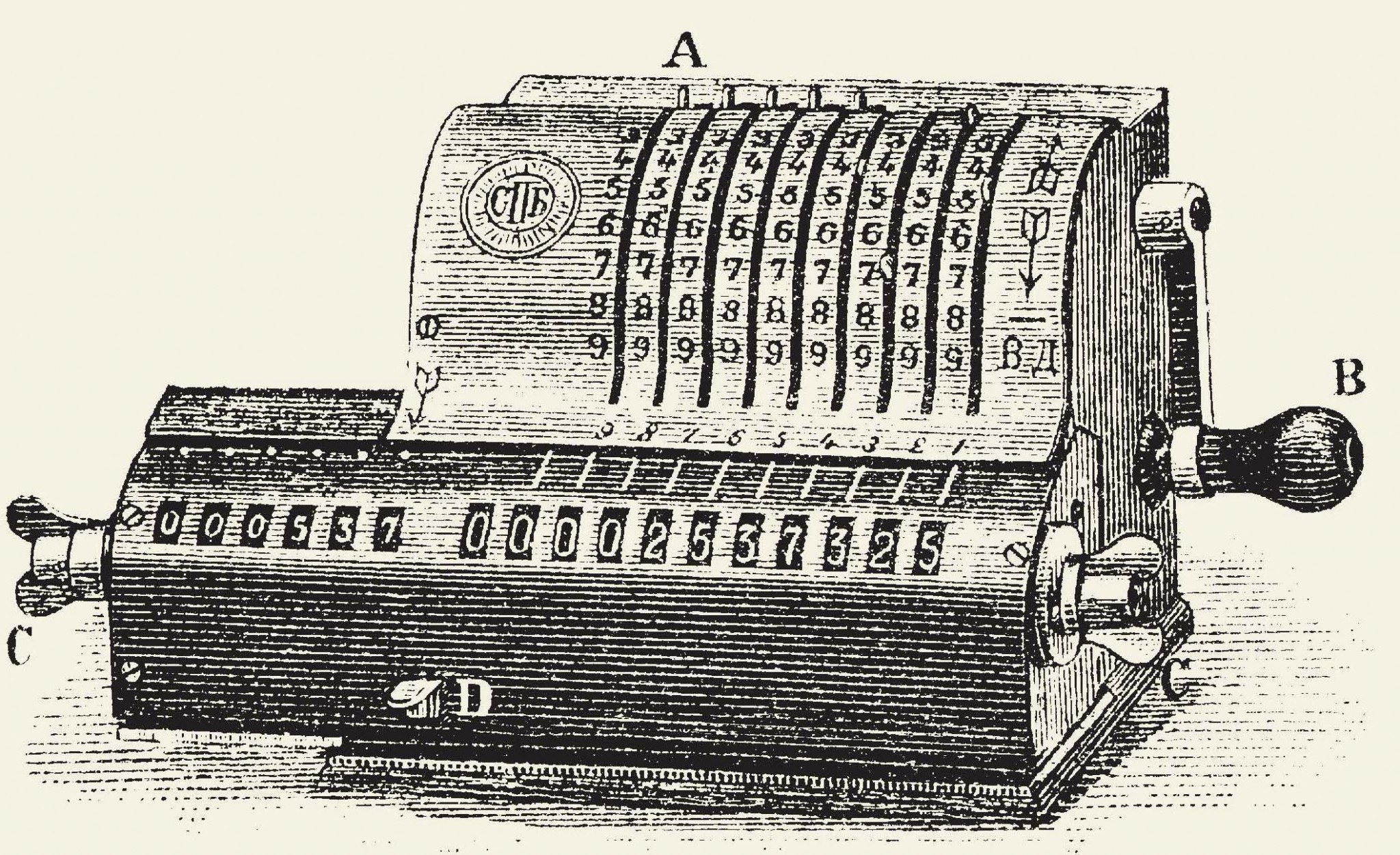
Написав статью об арифмометре Однера в 45-м номере «Науки и жизни» за 1890 год, автор (возможно, это был сам главный редактор и по совместительству изобретатель Матвей Никанорович Глубоковский) даже и не подозревал, что отметил рождение модели арифмометра, которой затем суждено было три четверти века доминировать в мире. Именно в 1890 году российский инженер шведского происхождения Вильгодт Теофилович Однер начал выпуск на своей небольшой фабрике новой модели счётной машины, которую он разрабатывал 15 лет. Что же нового внёс Однер в конструкцию арифмометра и как он к ней пришёл?
За двадцать лет до этого, в 1868 году, двадцатитрёхлетний студент Королевского технологического института в Стокгольме оправился покорять Санкт-Петербург с 8 рублями в кармане, подобно одному молодому гасконцу, который когда-то поехал покорять Париж с 8 экю. Его вдохновлял успех в России семьи шведов Нобелей. И так уж случилось, что в российской столице он стал работать на машиностроительном заводе Людвига Эммануиловича Нобеля, старшего брата знаменитого основателя Нобелевской премии. Молодой инженер, активно занимающийся самообразованием, пришёлся по душе Нобелю и, наверное, сделал бы на его заводе большую карьеру, если бы в дело не вмешался случай: в 1871 году его попросили отремонтировать арифмометр.
Счётные машины французского изобретателя Шарля Томаса (1785—1870) (сейчас принято писать Тома, но я буду использовать старое написание) в то время и до 1890 года были единственным массово выпускаемым механическим вычислительным устройством в мире. К 1870 году их было произведено около 1000 штук, и впоследствии они завоевали репутацию эталона этого вида техники. Их часто называли томас-машинами, хотя сам автор придумал для них название «Арифмометр», ставшее со временем названием всего рода вычислительных механических машин, способных выполнять все четыре арифметических действия. Отметим, что за создание арифмометра Томас получил степень офицера ордена Почётного легиона и стал именовать себя Томас де Кольмар.
Конструкция томас-машин была достаточно сложна, а изготовление деталей требовало высокой точности, так что ремонтировали их тогда только в одном месте — в Париже. История не сохранила нам имени человека, доверившего, возможно, по рекомендации Нобеля, ремонт столь дорогой машинки молодому инженеру, но он не прогадал. Однер не только сумел разобраться в устройстве, но и исправил его. Более того, как позднее написал сам Однер, он при этом пришёл к убеждению, что есть возможность более простым и целесообразным способом решить задачу механического исчисления.
Прежде, чем мы продолжим разговор о молодом изобретателе и его идее, попробуем понять, в чём заключается сам принцип механических вычислений, использованный Томасом, а затем и Однером. Тем, кого интересуют все существовавшие конструкции счётных машин, рекомендую замечательную монографию: И. А. Апокин, Л. Е. Майстров «История вычислительной техники: От простейших счётных приспособлений до сложных релейных систем» (М.: Наука, 1990), материалы из которой использованы в этой статье.
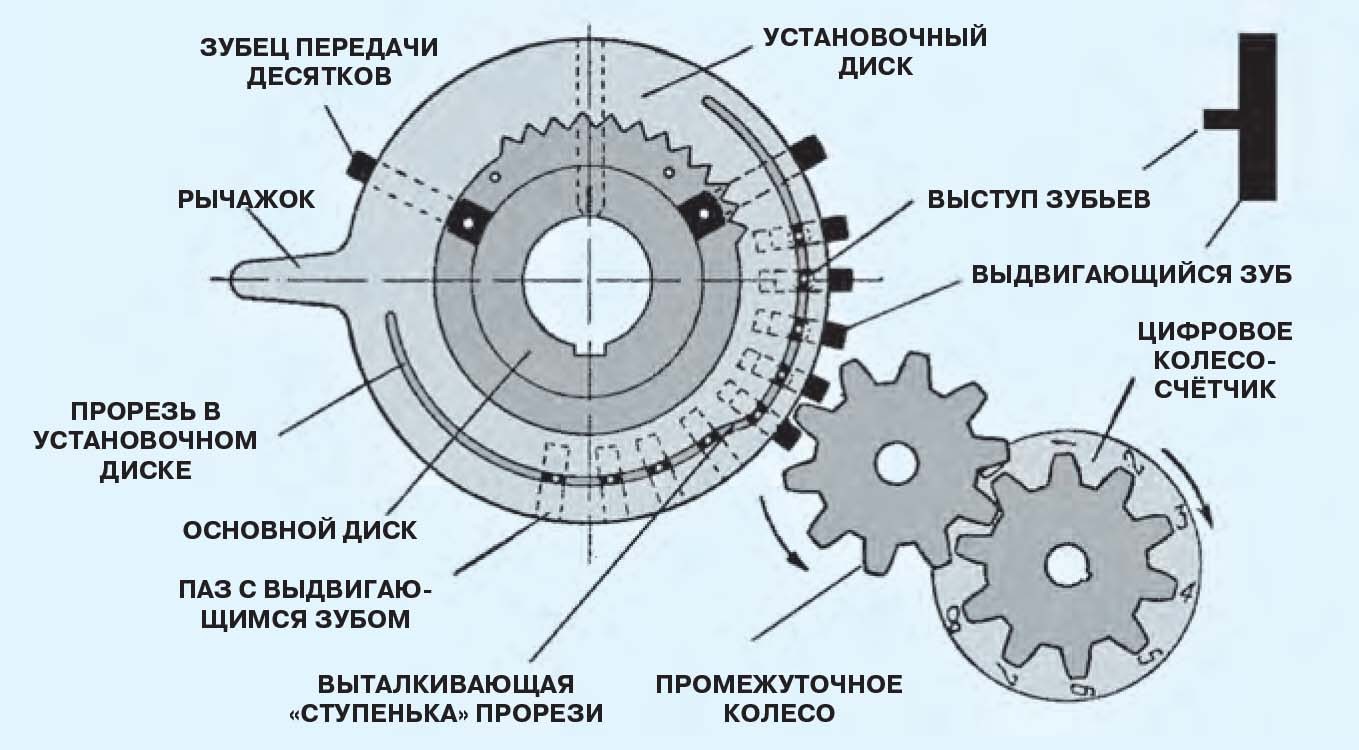
Итак, представим себе зубчатое колесосчётчик с десятью зубьями, с каждым из которых связана цифра, показываемая в окошке. Если изначально в окошке видна цифра 0, то, повернув колесо на три зуба, мы увидим в окошке уже цифру 3. А теперь, повернув колесо счётчика ещё на 4 зуба, мы увидим в окошке 3 + 4 = 7. Таким образом, реализуется сложение с помощью зубчатого колеса. Легко догадаться, что вычитание производится поворотом колеса в другую сторону. Например, 7 зубьев вперёд, а затем 5 назад, и в окошке появится 7 – 5 = 2. Умножение на целое число сводится к повтору поворотов: четыре раза по два зуба — и в окошке появится 2 х 4 = 8.
Для работы с многозначными числами надо собрать конструкцию из нескольких зубчатых колёс, каждое из которых соответствует своему разряду (единицы, десятки, сотни и т. д.). Надо только придумать механизм переноса десятков. То есть, когда первое колесо повернётся более, чем на 9 зубцов, второе должно повернуться на один. Вот здесь и возникают ещё две главные проблемы, помимо механизма передачи десятков, которые надо было решить конструкторам вычислительных машин.

Первая, как заставить каждое зубчатое колесо поворачиваться на своё количество зубьев, вращая их все вместе одной рукояткой. Совершенно очевидно, что вращать каждое колесо по отдельности нельзя, поскольку не будет выигрыша во времени счёта, точнее, наоборот, будет проигрыш, — проще считать на бумаге. Поэтому, например, умножить 357 на 8 надо всего за восемь поворотов рукоятки. При этом первое колесо каждый раз должно поворачиваться на 7 зубьев, второе — на 5, а третье — на 3. Вторая, как уменьшить число поворотов ручки при умножении. Понятно, что для умножения на 748 не хотелось бы делать 748 поворотов.
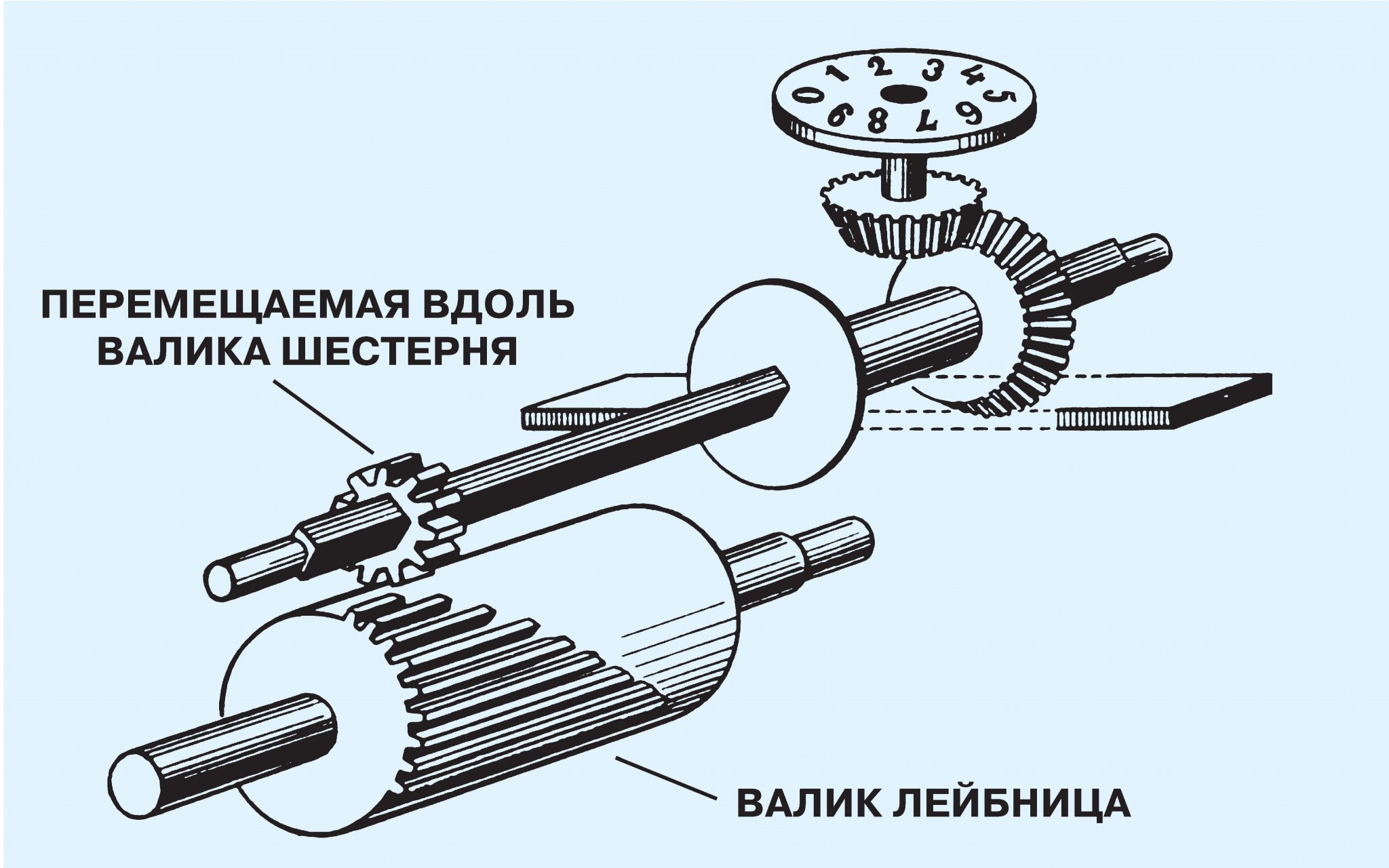
Хорошо работающее решение всех этих задач первым нашёл великий немецкий учёный-энциклопедист Готфрид Вильгельм Лейбниц (1646—1716). Для передачи чисел на колёса-счётчики Лейбниц придумал ступенчатый валик (см. рисунок). Ступеньки на валике, играющие роль зубьев, имели разную длину, поэтому, перемещая пере-дающую шестерню вдоль валика, можно было размещать её в зоне с разным числом ступенек. В начале валика под ней оказывались все 9 ступеней, и один оборот валика заставлял счётчик поворачиваться на 9 зубьев. Где-то в середине валика было, скажем, 5 ступеней, и один его оборот смещал счётчик уже на 5 зубьев. Таким образом, на каждом валике устанавливалась своя цифра числа, например, для числа 863 на первом валике передающая шестерня смещалась в область с 3 ступеньками, на втором — на 6, а на третьем — на 8. Теперь все валики одновременно поворачивались рукоятью и передавали на счётчик число 863.